TL;DR: A spatiotemporal continuous interpolation algorithm that reconstructs smooth geometry from a sparse and discrete sequence of independent point clouds.
Abstract
We introduce Canonical Consolidation Fields (CanFields). This novel method interpolates arbitrary-length sequences of independently sampled 3D point clouds into a unified, continuous, and coherent deforming shape. Unlike prior methods that oversmooth geometry or produce topological and geometric artifacts, CanFields optimizes fine-detailed geometry and deformation jointly in an unsupervised fitting with two novel bespoke modules. First, we introduce a dynamic consolidator module that adjusts the input and assigns confidence scores, balancing the optimization of the canonical shape and its motion. Second, we represent the motion as a diffeomorphic flow parameterized by a smooth velocity field. We have validated our robustness and accuracy on more than 50 diverse sequences, demonstrating its superior performance even with missing regions, noisy raw scans, and sparse data.
Pipeline
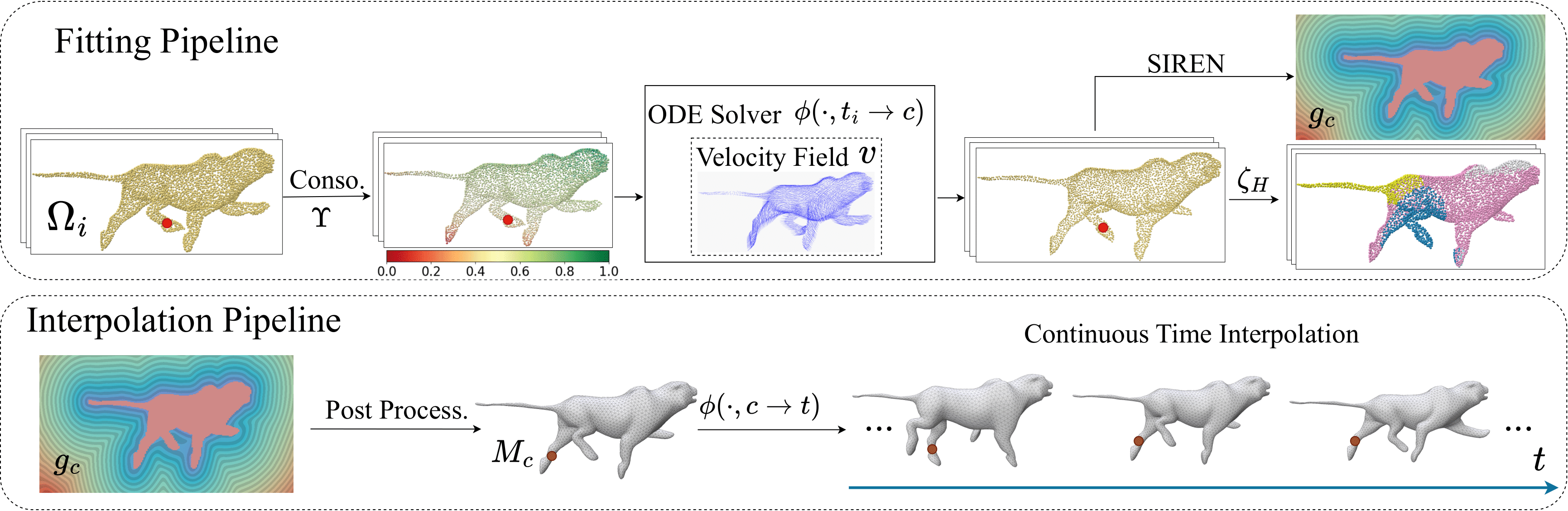
Top (Fitting Phase): The sampled input point clouds \( \Omega = \{\Omega_i\} \) are processed through our optimizable dynamic consolidator module \( \Upsilon \), reducing variance and estimating confidence. They are then input to the optimizable smooth velocity field \( v \), integrated by an ODE solver to the flow \( \phi \) that transforms points to the canonical time \( c \). An optimizable motion-segmentation network \( \zeta_H \) segments the points for articulation regularization. The reconstructed canonical implicit shape \( g_c \) is encoded with SIREN [Sitzmann et al. 2020].
Bottom (Interpolation Phase): We extract a mesh \( M_c \) of \( g_c \) with marching cubes [Lorensen and Cline 1987], and flow its vertices to obtain shape \( M_t \) for any target time \( t \).
BibTeX
@InProceedings{CanFields2025,
title={CanFields: Consolidating Diffeomorphic Flows for Non-Rigid 4D Interpolation
from Arbitrary-Length Sequences},
author={Wang, Miaowei and Li, Changjian and Vaxman, Amir},
booktitle={Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV)},
year={2025}}